非整数的阶乘
由Android计算器说起,简介非负实数的阶乘。

把 iPhone/iPod touch 横过来,或者使用 Android 内置计算器的高级功能可以进行阶乘计算。但有趣的是,当输入一个非整数的时候仍然会返回阶乘结果。
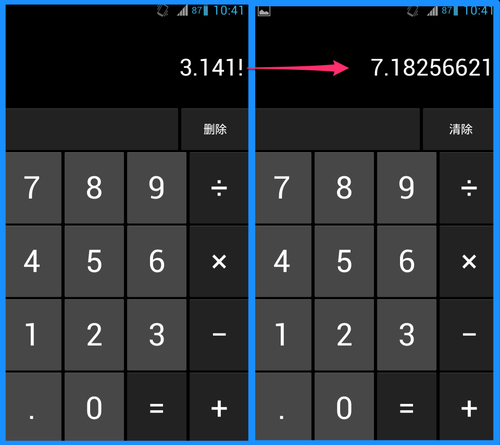
事实上,阶乘运算的原始定义如下(\( 0! = 1 \)):
$$n!=\prod_{k=1}^{n}k \qquad \big(\forall n \geq 1\big)$$
即是\( n! = 1 \times 2 \times 3 \times \cdots \times n \)。
对于非整数 z ,在非负实数域上,阶乘计算用 Gamma function(亦称 Γ 函数)扩展:
$$ z!=\Gamma\big(z+1\big)=\int_{0}^{\infty}t^{z}e^{-t}dt $$
对于工科学生,在概率论的计算的时候经常无意中偶遇这个函数。虽然不清楚这两个计算器内部的算法是什么,但我想计算器给出的结果符合 Γ 函数的定义。
关于阶乘和 Γ 函数的更多内容,推荐阅读:
- Wikipedia 阶乘的词条(英文版本的内容更加丰富):
http://zh.wikipedia.org/zh-cn/階乘 - Wikipedia - Gamma function:
http://en.wikipedia.org/wiki/Gamma_function